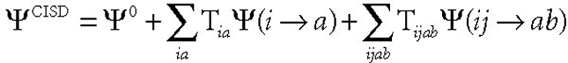
Wavefunction in Intermediate Normalization
These method keywords request a Hartree-Fock calculation followed by configuration interaction with all double substitutions (CID) or all single and double substitutions (CISD) from the Hartree-Fock reference determinant [Pople77, Raghavachari80a, Raghavachari81]. CI is a synonym for CISD.
FC
All frozen core options are available with this keyword. See the discussion of the FC options for full information.
Conver=N
Sets the convergence calculations to 10-N on the energy and 10-(N-2) on the wavefunction. The default is N=7 for single points and N=8 for gradients.
MaxCyc=n
Specifies the maximum number of cycles for CISD calculations.
SaveAmplitudes
Saves the converged amplitudes in the checkpoint file for use in a subsequent calculation (e.g., using a larger basis set). Using this option results in a very large checkpoint file, but also may significantly speed up later calculations.
ReadAmplitudes
Reads the converged amplitudes from the checkpoint file (if present). Note that the new calculation can use a different basis set, method (if applicable), etc. than the original one.
Energies, analytic gradients, and numerical frequencies.
Transformation
The CI energy appears in the output as follows:
DE(CI)= -.48299990D-01 E(CI)= -.75009023292D+02 NORM(A) = .10129586D+01
The output following the final CI iteration gives the predicted total energy. The second output line displays the value of Norm(A). Norm(A)–1 gives a measure of the correlation correction to the wavefunction; the coefficient of the HF configuration is thus 1/Norm(A). Note that the wavefunction is stored in intermediate normalization; that is:
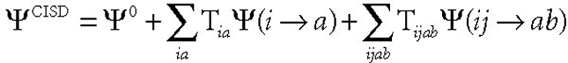
Wavefunction in Intermediate Normalization
where Ψ0 is the Hartree-Fock determinant and has a coefficient of 1 (which is what intermediate normalization means). Norm(A) is the factor by which to divide the wavefunction as given above to fully normalize it. Thus:
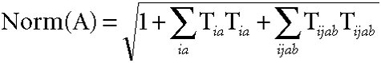
Fully Normalized Wavefunction
The coefficient of the Hartree-Fock determinant in the fully normalized wavefunction is then 1/Norm(A), the coefficient of singly-excited determinant Ψi→a is Tia/Norm(A), and so on.
Last updated on: 9 Jun 2009